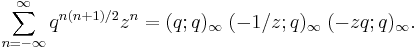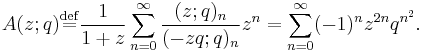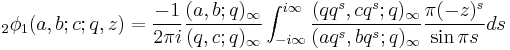Basic hypergeometric series
In mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series. A series xn is called hypergeometric if the ratio of successive terms xn+1/xn is a rational function of n. If the ratio of successive terms is a rational function of qn, then the series is called a basic hypergeometric series. The number q is called the base.
The basic hypergeometric series 2φ1(qα,qβ;qγ;q,x) was first considered by Eduard Heine (1846). It becomes the hypergeometric series F(α,β;γ;x) in the limit when the base q is 1.
Contents |
Definition
There are two forms of basic hypergeometric series, the unilateral basic hypergeometric series φ, and the more general bilateral basic geometric series ψ. The unilateral basic hypergeometric series is defined as
where
and where
is the q-shifted factorial. The most important special case is when j = k+1, when it becomes
This series is called balanced if a1...ak+1 = b1...bkq. This series is called well poised if a1q = a2b1 = ... = ak+1bk, and very well poised if in addition a2 = −a3 = qa11/2.
The bilateral basic hypergeometric series, corresponding to the bilateral hypergeometric series, is defined as
The most important special case is when j = k, when it becomes
The unilateral series can be obtained as a special case of the bilateral one by setting one of the b variables equal to q, at least when none of the a variables is a power of q., as all the terms with n<0 then vanish.
Simple series
Some simple series expressions include
and
and
The q-binomial theorem
The q-binomial theorem states that
which follows by repeatedly applying the identity
The special case of 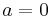 is closely related to the q-exponential.
is closely related to the q-exponential.
Ramanujan's identity
Ramanujan gave the identity
valid for 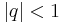 and
and 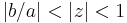 . Similar identities for
. Similar identities for 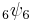 have been given by Bailey. Such identities can be understood to be generalizations of the Jacobi triple product theorem, which can be written using q-series as
have been given by Bailey. Such identities can be understood to be generalizations of the Jacobi triple product theorem, which can be written using q-series as
Ken Ono gives a related formal power series
Watson's contour integral
As an analogue of the Barnes integral for the hypergeometric series, Watson showed that
where the poles of 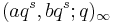 lie to the left of the contour and the remaining poles lie to the right. There is a similar contour integral for r+1φr. This contour integral gives an analytic continuation of the basic hypergeometric function in z.
lie to the left of the contour and the remaining poles lie to the right. There is a similar contour integral for r+1φr. This contour integral gives an analytic continuation of the basic hypergeometric function in z.
References
- Andrews, G. E. (2010), "q-Hypergeometric and Related Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/17
- W.N. Bailey, Generalized Hypergeometric Series, (1935) Cambridge Tracts in Mathematics and Mathematical Physics, No.32, Cambridge University Press, Cambridge.
- William Y. C. Chen and Amy Fu, Semi-Finite Forms of Bilateral Basic Hypergeometric Series (2004)
- Gwynneth H. Coogan and Ken Ono, A q-series identity and the Arithmetic of Hurwitz Zeta Functions, (2003) Proceedings of the American Mathematical Society 131, pp. 719–724
- Sylvie Corteel and Jeremy Lovejoy, Frobenius Partitions and the Combinatorics of Ramanujan's
 Summation
Summation - Fine, Nathan J. (1988), Basic hypergeometric series and applications, Mathematical Surveys and Monographs, 27, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1524-3, MR956465, http://www.ams.org/bookstore?fn=20&arg1=survseries&ikey=SURV-27
- Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications, 96 (2nd ed.), Cambridge University Press, doi:10.2277/0521833574, ISBN 978-0-521-83357-8, MR2128719
- Heine, Eduard (1846), "Über die Reihe
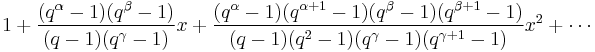 ", Journal für die reine und angewandte Mathematik 32: 210–212, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002145391
", Journal für die reine und angewandte Mathematik 32: 210–212, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002145391 - Eduard Heine, Theorie der Kugelfunctionen, (1878) 1, pp 97–125.
- Eduard Heine, Handbuch die Kugelfunctionen. Theorie und Anwendung (1898) Springer, Berlin.
![\;_{j}\phi_k \left[\begin{matrix}
a_1 & a_2 & \ldots & a_{j} \\
b_1 & b_2 & \ldots & b_k \end{matrix}
; q,z \right] = \sum_{n=0}^\infty
\frac {(a_1, a_2, \ldots, a_{j};q)_n} {(b_1, b_2, \ldots, b_k,q;q)_n} \left((-1)^nq^{n\choose 2}\right)^{1%2Bk-j}z^n](/2012-wikipedia_en_all_nopic_01_2012/I/2c3c423d7b1b9f3997f092b9a15925e9.png)
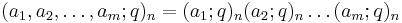
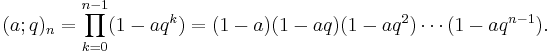
![\;_{k%2B1}\phi_k \left[\begin{matrix}
a_1 & a_2 & \ldots & a_{k}&a_{k%2B1} \\
b_1 & b_2 & \ldots & b_{k} \end{matrix}
; q,z \right] = \sum_{n=0}^\infty
\frac {(a_1, a_2, \ldots, a_{k%2B1};q)_n} {(b_1, b_2, \ldots, b_k,q;q)_n} z^n.](/2012-wikipedia_en_all_nopic_01_2012/I/819728b8a13606dfb51a8a4257376806.png)
![\;_j\psi_k \left[\begin{matrix}
a_1 & a_2 & \ldots & a_j \\
b_1 & b_2 & \ldots & b_k \end{matrix}
; q,z \right] = \sum_{n=-\infty}^\infty
\frac {(a_1, a_2, \ldots, a_j;q)_n} {(b_1, b_2, \ldots, b_k;q)_n} \left((-1)^nq^{n\choose 2}\right)^{k-j}z^n.](/2012-wikipedia_en_all_nopic_01_2012/I/0a0998915eaf9112cd573f4ea7c80043.png)
![\;_k\psi_k \left[\begin{matrix}
a_1 & a_2 & \ldots & a_k \\
b_1 & b_2 & \ldots & b_k \end{matrix}
; q,z \right] = \sum_{n=-\infty}^\infty
\frac {(a_1, a_2, \ldots, a_k;q)_n} {(b_1, b_2, \ldots, b_k;q)_n} z^n.](/2012-wikipedia_en_all_nopic_01_2012/I/2f52a9ddbb6b83ac7b1f6aa873bdce01.png)
![\frac{z}{1-q} \;_{2}\phi_1 \left[\begin{matrix}
q \; q \\
q^2 \end{matrix}\; �; q,z \right] =
\frac{z}{1-q}
%2B \frac{z^2}{1-q^2}
%2B \frac{z^3}{1-q^3}
%2B \ldots](/2012-wikipedia_en_all_nopic_01_2012/I/7e8df00949af12cfad161caaacbe12f5.png)
![\frac{z}{1-q^{1/2}} \;_{2}\phi_1 \left[\begin{matrix}
q \; q^{1/2} \\
q^{3/2} \end{matrix}\; �; q,z \right] =
\frac{z}{1-q^{1/2}}
%2B \frac{z^2}{1-q^{3/2}}
%2B \frac{z^3}{1-q^{5/2}}
%2B \ldots](/2012-wikipedia_en_all_nopic_01_2012/I/1cfa9f8cfcd4b2965a0594635e0d9e50.png)
![\;_{2}\phi_1 \left[\begin{matrix}
q \; -1 \\
-q \end{matrix}\; �; q,z \right] = 1%2B
\frac{2z}{1%2Bq}
%2B \frac{2z^2}{1%2Bq^2}
%2B \frac{2z^3}{1%2Bq^3}
%2B \ldots.](/2012-wikipedia_en_all_nopic_01_2012/I/523611058a40eedf1dd82fdae8c7ddc1.png)
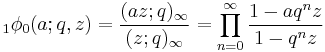
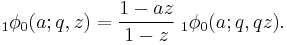
![\;_1\psi_1 \left[\begin{matrix} a \\ b \end{matrix}�; q,z \right]
= \sum_{n=-\infty}^\infty \frac {(a;q)_n} {(b;q)_n} z^n
= \frac {(b/a,q,q/az,az;q)_\infty }
{(b,b/az,q/a,z;q)_\infty}](/2012-wikipedia_en_all_nopic_01_2012/I/81e1af24c6d0fb01514c3130bdd6f5a3.png)